|
|
|

|







|
|
  |
CLICK HERE FOR AN MORE UP TO DATE AND BANNER FREE VERSION News from the front (25 September 2001)The source code of SGPO might well be lost... However we still have an old version of it that is not compatible but is working the same way. I found the necessary tool to handel PNG in C(++). So I might well also find the time to make a similar program for PNG file. I found a similar program in the name of Gifshuffle. Gifshuffle also offer build in encryption and compression. I guess if it can be disabled then maybe it will be "compatible" with SGPO. If it is not then maybe the new version of SGPO will be. "SteganoGifPaletteOrder"(Hiding data into the palette of a GIF file)Executive summaryIf you did find this page a bit randomly, those first few line should help you figure out if you want to read the rest:"This page explain the trick in use by our program (and how to use our program) to hide data within a GIF file." Where are those data hidden ?The data we want to hide are store into the palette of a GIF file. The picture is in no way modify, just the order of the color within the palette is slightly modify in order to keep our secret message. The compression or size of the file won't be change at all. A viewer won't be able to know what are the change. Of course, someone with the program will be able to retreave the secret message. And someone looking at the right place might notice that the order of the color within the palette is a be unusual (at least not sorted).What do the program do ?There are two basic function for the program. One is to generate a graphic file where there is an hidden message and the other is to retrieve the message witch is incorporated into the graphic file.Because there is absolutely no secret within the method we use, anybody can retrieve the message if he have the program/knowledge. It is possible to retrieve something from a graphic file where nothing have been hidden. Of course, this thing won't be anything intelligent. It's up to the person extracting the message to figure out if this is a message or just some trash. If you have something to hide and want to protect your message, then you better have to send an encrypted hidden message and make sure your encryption program put as few structure as possible into the encrypted message so that it will be difficult to recognize that this is an encrypted message. If you want to compress your message, make sure this is the first operation you do, then only encrypt and finally hide the result into a graphic file. Because encryption introduce confusion within your data, it will be very hard to compress after. As a matter of fact, a steganographic technique should also provide a build in encryption algorithm so that the knowledge of the technique is not the only secret (as for security by obscurity). The method we have implemented can provide this build in encryption with almost no extra cost (in space not in cpu time). The encryption is to my knowledge very strong if the length of the key is as long as the length of the message. It should be equivalent to use an XOR between your message and the key before trying to hide the message. The encryption is not yet implemented... You can safely skip a few paragraph if you only want to just use the program. Let's get to the technical side.The hidden message will be put inside the palette part of a graphic file. As the order of the color into the palette is not important for the rendering of the image, data can be hidden into the permutation of the color inside this palette.For graphic file that use a palette, this palette is a table of color. Then, every pixel is represented as an index to this table. The trick is to change the order of the color into the palette and also change every reference to the new index after permutation. So we will encode our hidden message into a permutation. With a palette of 256 color, we have factorial of 256 possible permutation. As we will translate a message into a permutation, we will be able to hide as much as factorial of 256 possible different message. All of those message will have an associated permutation. We will be able to also make the reverse mapping, from the permutation to the message. As we need to be able identify the permutation that have been used, we need a reference order for the color into the palette. So before you apply a permutation, you need to "sort" the palette into a reference representation. From there, you can apply the permutation to the new sorted palette. Your message have now been hidden. On the other side, to get back the message, we will have to sort the palette and figure out the permutation to get from the sorted palette to the palette we received. Some kind of reverse permutation. The using the reverse mapping we can find back the message that was hidden and it will be clear text for us. A few question still need to be answered to fully understand how it actually work within our implementation. You need to know how we get from a message to a permutation and then back to the message again. We will explain more in detail the process and algorithm to implement this technique. From a message to a permutation.We will put an extra step between a message and the permutation. We will numbered all the permutation and we will use an algorithm that will generate from any number between 0 and (n!)-1 a permutation. Also, from the permutation we need to be able to reverse the process. Now we need to map a message to a number between 0 and n!-1. And we need to reverse the process.From a message to a number (and from this number back to a message).To stay as general as possible, we need to assume that the message is a stream of bit at zero and one, and size of that stream is not fixed. If the message is a string, then we will use binary representation of all those character from the string. From a stream of bit it's easy to get to a number, we just have to consider that we have the binary representation of our number. We also need to be able to differentiate those two message 101101 and 0101101 that both map to 45. In fact we need to encode the length of the message to be able to get back to the original one. To do that we will always put a leading one in front of this stream of byte. On the other side we juste have to remove this extra bit. So those previous message will be coded 1101101 and 10101101 witch map respectively to 109 and 173. So we only use one bit to encode the size of the message.Most of the time, our message is only made of stream of byte, then we will put them in the Most Significant Bit First order and the byte/character 'A', which have position 65 into ASCII character set and 65 have the binary representation '01000001', will be encoded 101000001 (so 321 which is 65 + 256). As a matter of fact, the empty message will be encoded as 1. Because there is no message associate with the value 0, we will always remove one to the encoding of the message. So now the empty message will be a value of 0 and 'A' will be a value of 320. So on a practical point of view we start with one into an accumulator and for every byte/character from the message, we add the value of that byte to the accumulator multiply by 256 (except for the last byte). At the end we remove one from the big value we get. To decode the message we first add one to the value. Then we just have to compute the remain from dividing by 256, which is the last character. Then divide again (and keep the remain) for the previous one, and again until we get one or zero. If we get to one then this is a message with a size multiple of 8. Otherwise, the last byte we get is to be decoded into a certain number of bit from one to seven to be further analyze. No big deal, we will work with stream of byte even if this could be a weakness (as we don't use all possible permutation). From a number to a permutation (and from this permutation back to a number).Well, this is maybe the most difficult part. Hopefully Didier Barzin did manage to find an algorithm to generate a permutation from a number and way back. This is not fast because we are working with very big number, but it is working. And if you want to make compatible program, you will have to implement a similar algorithm.A permutation is always a permutation of something, so we need to know how much 'distinct' element we have available. So how much color we have in the palette. We will suppose that the palette contain only unique color. We also need to make sure the number we want to encode is lower than factorial of this number of element. We won't work with permutation of a set of element where you have duplicate because in a palette of color you should not find any duplicate. But it could be interesting to work on this problem... We need to consider the permutation in an other way in order to simplify the algorithm. If you create a permutation of height element (the number between zero and seven) then for your first index you have height possibility, for the next one, you must choose between the seven left possibilities, then the six left… until your last choice is forced. So we can see this permutation with number within those range (0..7, 0..6, 0..5, 0..4, 0..3, 0..2, 0..1, 0). And this make 8*7*6*5*4*3*2*1 possibilities (witch is what we expect). To get from a number to a representation like that we just have to divide our number by height, then we have left by seven, … To get from this representation of a permutation to a number, we can just apply reverse rule. You take the last number (always zero) and multiply by the number of element, then add the previous one and multiply by the number of element minus one, and continue until you get to add the first element that we multiply by one. To terminate the story of our code, it seems that we work on element starting with the last one. So our range of value move that way: (0, 0..1, 0..2, 0..3, 0..4, 0..5, 0..6, 0..7). We will continue to explain using our representation. If I find the name of this algorithm, I'll let you know. But this is well known and you can find it in almost any excellent algorithm book. From our representation of a permutation to a useful one.Well, this is the piece of code we use to go from our representation of a permutation to one where every number between one and n are represented only once. In this code n is the number of element into this vector and v[0..(n-1)] is our permutation vector (i and j are loop index) :for (int i=0; i<s; i++) for (int j=0; j<i; j++) if (v[j]>=v[i]) v[j]++;To get back from a permutation to our own representation, we use the following piece of code: for (int i=s-1;i>=0;i--) for (int j=0;j<i;j++) if (v[j]>=v[i]) v[j]--;Well, this is some kind of magic to me… I will let you figure out yourself how this can work and give what we expect. We will apply multiple permutation on the set of data in order to create some kind of build in cryptography. One permutation is suppose to hide the other one. As a result of test with the effect of multiple permutation, I discovered a small flaw in the way our permutation where generate. For a small number, you get a permutation like this (7,6,5,4,3,0,2,1). Where what was on the top go to the bottom and what was at the bottom get to the top with some permutation. Then if you apply a second permutation of that kind, coming from another small number, you won't get overlapping permutation but the central value stay fix and separate permutation of the top and bottom of the set. For the set (A,B,C,D,E,F,G,H) you may get (C,B,A,D,E,G,H,F) where D and E don't move and you easily distinguish both permutation of ABC and FGH. In order to make those to permutation overlap, we will reverse our permutation to get from (7,6,5,4,3,0,2,1) to (1,2,0,3,4,5,6,7). The smaller the number, the less we will mix the end of the set. For the number zero, we will have the 'no change' permutation (0,1,2,3,4,5,6,7). This mean an empty message will just sort the palette (or keep it the same way) of your graphic file (nice side effect). If you read carefully the next paragraph, you will notice that if you put an empty encryption message, it's just like making no encryption at all (another useful side effect). More on that, if you want to really "secure" your "hidden" text, you need to provide an encryption message key bigger (in size) than your message. Adding cryptography to the process (not yet implemented).We can argue on whether or not encryption should be part of the steganographic process. In our case we can have "build in" encryption at almost no cost. Rather than to use the sorted palette as a reference permutation of the palette, we can start with a sorted palette and apply a secret permutation based on a secret message. Then only we apply the "hidden text" permutation. This is like hiding two messages at the same place. One on top of the other one. Like an XOR between the hidden message and the secret message. Of course for the secret message is to be change often, otherwise it will loose it's strength. Also if the clear text and hidden message are to be known, then the secret is not a secret anymore. Maybe the secret (or encryption) message should be generate from a random number generator based on a secret key and a cryptographic algorithm...Whatever, we offer you the option to enter two messages, one to hide and one to serve as a secret key. If you don't use this optional key, then anyone with the program will be able to recover your hidden message. If you use the key, make sure the person on the other side share this secret with you. You can be pretty confident that no one will be able to recover your message without the key (or the key without the clear text message). I hope this option won't stop you to use other cryptographic tools in order to sign or encrypt (your usual way) your message. More is to be done on this "encryption". Is it useful? What if you use multiple time the same secret? Is it better, equal or worse than just doing an XOR between the 'secret key' and the 'message to hide' before the permutation process? What if you use a too small 'secret key', will it make some part of the message 'easy' to recover and then which part, beginning or the end? I'll let you work on those question, I already have some answer. I just like the fact that we can apply a permutation on a permutation. Also, there is no reason to call one of the permutation the message or the secret. This way you hide two message into something and anybody knowing one of them can find the other one. This is just for fun. Some other glory details you don't want to know.I needed to write this somewhere in order to have it handy when my head start to hurt wondering about undocumented detail of our code. This project lasted for almost a year. This is because of : the lack of time, some other personal project going on, the difficulty to read/write GIF, the need of a BigInteger module, the portability issue, trouble to coordinate the two author. In fact, as soon as we got the idea, then the algorithm, then something working we where almost happy. We finally manage to get some user interface and to incorporate GIF reading/writing into a program. This file is also the best we can offer for the documentation of this program.Working with permutation (and reverse permutation).Well, it is always a trouble for me to remember how we work with permutation. This is because there is two way to consider a permutation vector. Maybe it is more a religion issue because it is easy to go from one permutation to the reverse representation.For me a permutation is a vector of index value where every number from one to the maximum number is represented once and only once. The vector (3,1,2,5,4) is thus a permutation because it contain five elements from one to five and those elements are represented once and only one. This permutation tell us that data element in position one should be put in position three, data element in position two should be put in position one, … Let's apply this permutation to the sorted data vector (A,B,C,D,E): The sorted data vector : A B C D E The permutation vector : 3 1 2 5 4 The permutation applied on the data : B C A E DNow once we have the permuted data, how can we figure out witch was the permutation applied? Well, it is quiet easy, we just have to mark every element of the permuted data with their position from one to five in the vector. The we can sort the data and this will give us the permutation we are looking for. The marked data : B1 C2 A3 E4 D5 Sorted marked data : A3 B1 C2 D5 E4 The permutation we where looking for : 3 1 2 5 4Ok, so now can we figure out witch is the reverse permutation to get back from (B,C,A,E,D) to (A,B,C,D,E)? In fact this is really easy, we just have to apply the permutation to the set of data (1,2,3,4,5) with number from one to five. The sorted data vector : "1" "2" "3" "4" "5" The permutation vector : 3 1 2 5 4 The permutation applied on the data : "2" "3" "1" "5" "4" The reverse permutation we found : 2 3 1 5 4We can now apply this reverse permutation on the permuted data in order to check that we have what we expect. The permuted data : B C A E D The reverse permutation : 2 3 1 5 4 The applied reverse permutation : A B C D EI hope those example will help you understand how we can work with permutation, apply them and find them back. To confuse the discussion, there is an other way to consider a permutation vector, witch is just like applying reverse permutation… You will read something like (3,1,2,5,4) as fill first position with element in position number three, fill second position with element in position number one, … The sorted data vector : A B C D E The permutation vector : 3 1 2 5 4 The permutation applied on the data : C A B E DWhich is exactly the result we get if we apply reverse permutation in the way we did previously. The sorted data vector : A B C D E The reverse permutation : 2 3 1 5 4 The permutation applied on the data : C A B E DSo now you know everything there is to know about permutation. Chose your way to work with those permutation vector. I don't know if any of those two symmetrical way is standardize, I will have to ask the closest mathematician I know. Apply two permutation (the permutation of a permutation ?).As the code improve, or degenerate, I was confronted with the need to be able to apply two permutation in one time. This was useful for applying first the KEY permutation and then the MSG permutation. Because the new API we use for makingGIF only accept one permutation, I needed to figure out how to merge them together. Let's have two permutation:
and apply those permutations to the sorted data vector (A,B,C,D,E):
So the merged permutation is:
Well, I don't know how to explain that to you, but to find the combine
permutation, I just have to apply the reverse permutation of the first
one to the second one:
This is not all, but I still have to work (again) on the encryption stuff so I will sort it out and try to make it work once and for all. GIF files in and out.To be able to use this kind of technique of steganography, we need a graphic format that support image with a palette of color. GIF is certainly not the best graphic format, but it is well known and supported (even if it use a patented compression algorithm). As a matter of fact our program will have to decode a GIF file, apply our hiding algorithm and finally generate a new GIF file with a permuted palette. For the decoding process, we only need to read the palette of the GIF file, so this can be done in a more easy way. Java offer us build in capability to display a GIF file, but you don't have everything we needed for our program.Let's have a look at problem we encounter with GIF file.A GIF file support a palette with a palette from two color to a palette with 256 color, but the number of color must be a power of two (2, 4, 8, 16, 32, 64, 128 or 256). This mean if we have 130 different color into our picture, we will have to use a 256 color palette size. We may have to generate unique unused missing color. We need those color to be unique in order to be able to sort the color into the palette as a reference permutation. This could be identify because, more likely, other graphic program just zero those color if they are not in use.There are multiple reference to the palette index into a GIF file, not only the pixel. We also have a Background color and a potential transparent color into GIF89. So we will have to also modify those reference once the palette have been permuted. Also into a GIF file there might be more than one picture or piece of picture and for all those picture, we can have different palette, global palette and local palette. Those option are use mostly for 'animated' GIF file but might be encounter at some other place. A GIF file can also hold all kind of chunk of data, like a text comment, including proprietary chunk. A GIF file can be interlaced picture to do progressive display while downloading the file. So there are many thing to implement in order to be able to fully support GIF. We don't implement all of these. Because we will decode GIF file generate by our own code and we control the way we generate those GIF file, we will restrict ourselves to a subset of the standard. Most GIF feature won't be available to you with our program. Of course you can manually use the generated palette and apply it to your GIF file with fancy feature. In the future, we might remove the GIF decompression algorithm and use the one available into AWT. That way the input file won't have to be a GIF file and any format supported by AWT in witch we can find a number of color smaller or equal to 256 is ok for us. Of course the output will always be a GIF, except if we implement also PNG. Download the programThis is the only place where you can download this program from.Install and run the program (this is what you are looking for)The program is a java application with graphical interface that need java 1.1.It is distributed as a zip file that contain every .class file you need to make it run, a copy of this documentation, and a few GIF file with encoded message. Those files should never be separated. To install, just unzip everything into one newly created directory. To execute the program, you need JDK1.1 or the any java 1.1 runtime environment. The "file" to run is SteganoGifPaletteOrder.class with command line like 'java SteganoGifPaletteOrder'. A little knowledge of java might help to do that. Using the programWe basically have three zone: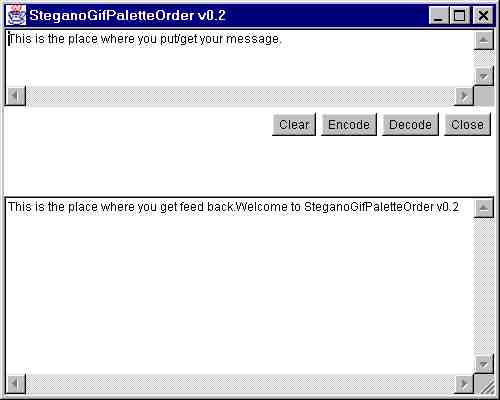
The output file is always "out.gif" in the same directory you readed the input file from. The program don't check that your input palette is big enough to contain your hidden message. The program simply don't check anything at all. The program might crash if: It don't recognize it is a GIF, find unexpected input, ... Future development...This chapter is about thing we won't have time to do. And I need to tell you that it took us quiet some time between the original idea and it's final implementation. So I don't expect to spend that much more time on this project. Of course it always help to get some feedback from user and other person interested in steganography.I would like to have support for PNG file format as this format use an open compression algorithm witch is patent free. Also this seems to be the format of the future of the World Wide Web, at least as soon as your favorite browser will support this and/or Web server will be able to serve in a different way clients with different capabilities. Java is portable, but it would be nice to have a complete C/C++ version of this code, including support for big integer and compression/decompression of the mostly used graphic file that support palette. This way we could have a highly optimized version of the code because this is a bit CPU intensive and java does not help. I would like to write a Palm Pilot version of this code because this is more likely to be my next development platform. I need to clean-up the code a little bit. I need to clean up this documentation and the "distribution" (installation, pointer to JDK, ...) of the program. A wintel.exe could be nice. Encryption is definitively needed as a must. I would like to also make available a java applet (my text file palette version would do the trick). Also I am looking for other place where 'steganography by permutation' can be apply. Any file format sufficiently standardize, open and used on the internet or for electronic exchange that support chunk of data that can be sorted and reordered without lost of information will do the trick. Of course because this is free time programming it is more likely that we won't have time to provide support and that we can not provide any warranty for the usefulness and workability of this program. Author (and credit where credit is due).We are two to program on this stuff, and we can be reach by e-mail and have our web home page:David GLAUDE: glu@who.net. Didier BARZIN: didier@unforgettable.com. Somebody did made a nice web page explaining the hiding permutation concept. I did read it long ago, but after I got the idea myself. Whatever, the algorithm was missing and we have a working implementation. As soon as I find the URL for this page, I will update this page. Somebody did discover the algorithm we use for making the permutation, so if I find out, I will document, make a reference to the book or just give the name of the algorithm (if any). We used the code of someone for everything which is GIF encoding/decoding related (we did modify it a bit): // GifEncoder - write out an image as a GIF // // Transparency handling and variable bit size courtesy of Jack Palevich. // // Copyright (C)1996,1998 by Jef Poskanzer <jef@acme.com>. All rights reserved. // ImageEncoder - abstract class for writing out an image
// Redistribution and use in source and binary forms, with or without
As for the ``AS IS´´ concept, this also apply for the rest
of the code.
Copyright, source code, do and don't,...We keep our right on the program, source code, ...You can freely: use, download, redistribute free of charge as a whole without modification. You can not: modify, remove credit where credit is due, disassemble java byte code, earn money selling our code. Don't ask for the source code, it's not yet available we still have to clean it up, implement other feature, ... Don't ask for help to install, use, ... the program (except if it's not working and it's not your fault) RTFM. Don't use our code for illegal stuff in your country. We will work out another policy (GNU, artistic license, BSD like, open software, ...) as soon as we agree on something we both feel conformable with. 2000 UpdateGiven the current problem with GIF pattend, it is more likely that this program is illegal... This program could be adapted for PNG input and output and use PNGLib, but this was just a proof of concept. |
|
| 20892 | The content of this page is copyrighted: ©David GLAUDE. |